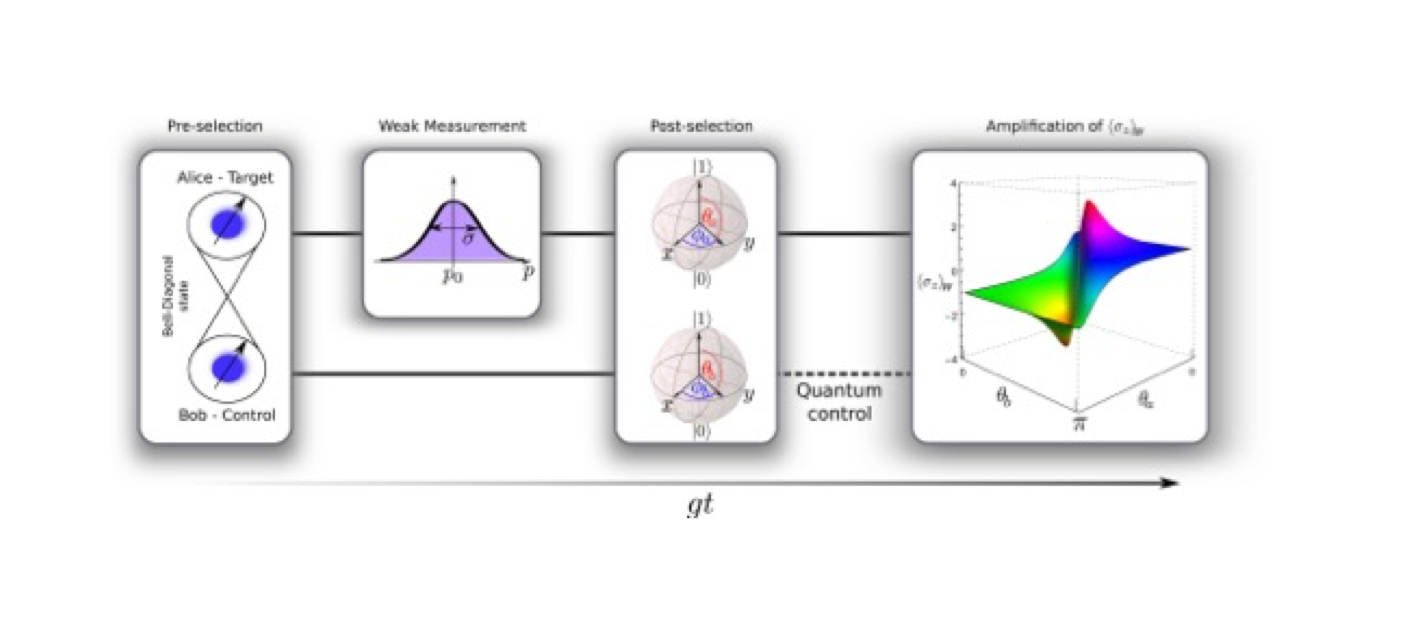
En las medidas débiles, una teoría desarrollada por Aharonov y colaboradores [1], el fuerte impacto de una medida tipo Von Neumann es drásticamente reducido, dado que esta consiste en la acumulación gradual de información entre el sistema y el medidor durante un tiempo finito de interacción. En la referencia de más arriba, ellos muestran que la combinación de una medida débil seguida de una fuerte post-selección puede conducir a la amplificación, en el sentido que el valor medio inferido del sistema medido puede ser mucho mayor que cualquiera de sus valores propios.
Estamos muy interesados en las aplicaciones en el contexto de la cavidad qed, optomecánica, spin-mecánica. Por ejemplo, estudiamos:
a) la amplificación de valor débil de los operadores de número de fotones en un interferómetro Michelson,
b) creación de estados fotónicos cuánticos usando un interferómetro Ramsey seguido por una post-selección,
c) enfriar una distribución de fotones en una cavidad o una distribución de fonones en un sistema spin-mecánico.
d) Otras aplicaciones como detección de ondas gravitacionales, amplificación de señales muy pequeñas, etc.

[1] Y. Aharonov, D. Z. Albert, L. Vaidman, “How the result of a measurement of a component of a spin ½ can turn out to be 100”, Phys. Rev. Lett, 60, 1351 (1988).