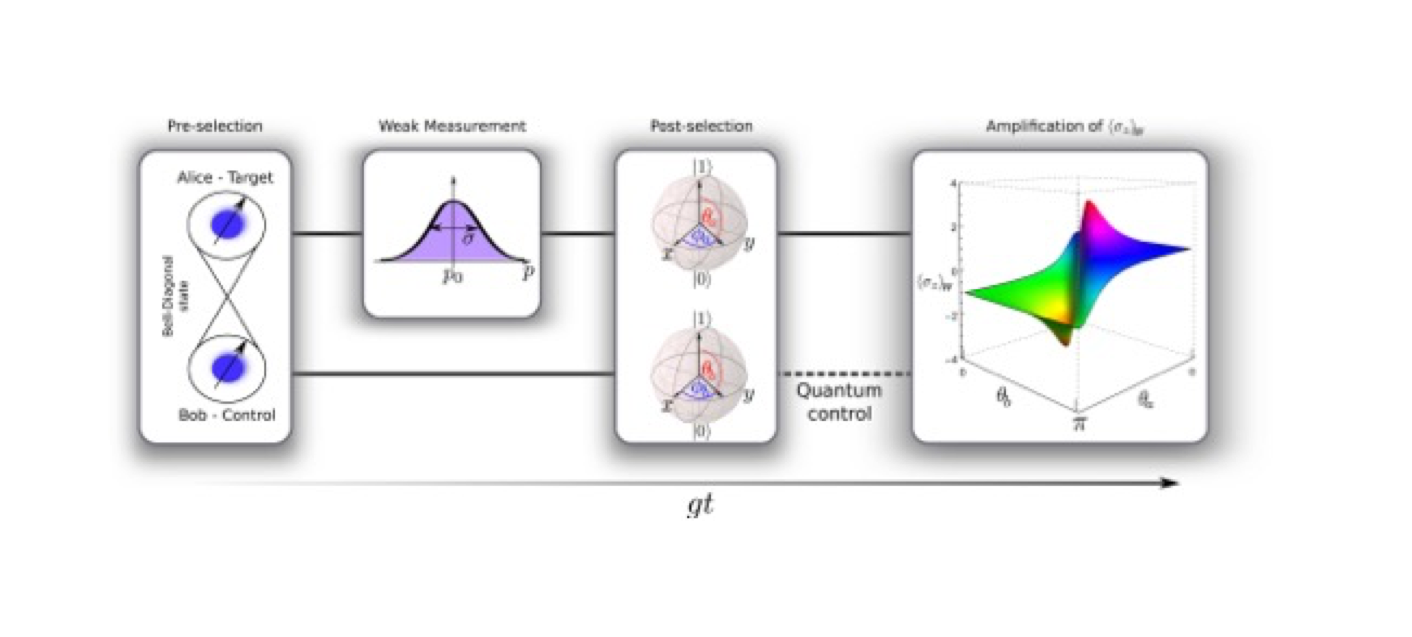
In Weak Measurements, a theory developed by Aharonov and collaborators [1], the strong impact of Von Neumann type of measurement is drastically reduced, since it consists of gradual accumulation of information during a finite interaction time between the system and the meter.

In the above reference, they showed that the combination of weak measurement followed by a strong post-selection may lead to amplification, in the sense that the inferred mean value of the measured system may be much larger than any of its eigenvalues.

We are strongly interested in applications of this amplification in the context of cavity qed, opto-mechanics and spin-mechanics. For example, we study:

a) weak value amplification of the photon number operators in a Michelson interferometer,

b) creation of quantum photonic states using a Ramsey interferometer followed by post- selection,

c) cooling a photon distribution in a cavity or a phonon distribution in a spin-mechanical system.

d) Other applications such as detection of gravitational waves, amplification of ultra-small signals, etc.

[1] Y. Aharonov, D. Z. Albert, L. Vaidman, “How the result of a measurement of a component of a spin ½ can turn out to be 100”, Phys. Rev. Lett, 60, 1351 (1988).